- We weten al wat de reactantie van een condensator of spoel is. We zagen tevens het gedrag van een zuivere wisselspanning op een weerstand.
- Hieruit onthouden we dat een zuivere weerstand GEEN defasering tussen stroom en spanning veroorzaakt, maar een condensator en spoel wél.
- Tot nu werden enkel op zichzelf staande componenten bekeken. Wat gebeurt er als we de drie elementen combineren.?
Het combineren van spoelen, condensatoren en weerstanden in serie en/of in parallel brengt ons tot schakelingen die in het domein van de radio zeer veel worden gebruikt. Zo een kring vormt dan een impedantie die zich op het vlak van wisselstroom op een nuttige en gewenste manier gedraagt. Door deze elementen op een bepaalde manier te combineren reageren ze op de wisselstroom.
Intuïtief voel je aan dat condensatoren en spoelen tegengesteld reageren op stroom of spanning. De driehoeksmeetkunde en Pythagoras gaan ons helpen om dit fenomeen te begrijpen.
De impedantie wordt als Z genoteerd en in Ω uitgedrukt.
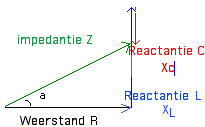
in het zwart : de weerstand R
in het blauw : de reactantie van de spoel XL
in het rood : de reactantie van de condensator XC
in het groen : de impedantie van de kring Z
Uitleg
We hebben de capacitieve en Xc spoelreactanties Xl uitgerekend en ze zijn ons bekend voor een welbepaalde frequentie van het aangelegde signaal. Hiermee kunnen we bij de figuur hiernaast de vectoriële som uitvoeren.
Vectoren optellen is vrij eenvoudig door alle vectorïele voorstellingen de één na de andere aan elk uiteinde te tekenen. Bekijken we de grafiek nader.
De verschillende vectoren worden door een verschillende kleur voorgesteld. De lengte van een vector is proportioneel met de grootte van de voorgestelde waarde.
Als we de as van de weerstand r als referentie nemen moeten we ook de fase “nul” hieraan toekennen. Uit wat vooraf ging weten we dat de reactanties hier met 90 ° op staan.
De blauwe vector stelt de inductieve reactantie voor en wijst daarom naar boven. Daartegenover staat de rode vector voor de capaciteit, hij wijst tegengesteld aan die van de spoel. Te opzichte van r is dit ook 90 °. De lengten worden bepaald door hun waarden.
De capacitieve reactantie wordt van de inductieve afgetrokken. Aftrekken wordt ook wel algebraïsch samentellen ( rekening houden met het teken ). Het uiteindelijk gedrag van Z wordt door de dominante samenstelling bepaald.
In ons voorbeeld is Z dus duidelijk inductief van gedrag.
De hoek “a” verwijst naar de defasering tussen spanning en stroom. ( Merk op dat het hier niet meer om de 90 ° gaat). Natuurlijk kan men Z op nog andere manieren berekenen. Grafisch met driehoeksmeetkunde kan het ook ( bepalen van de hypotenusa ).
Verwarring
Spreken van de impedantie van een condensator of spoel is eigenlijk fout. Hun “tegenstand” aan de stroom noemen we beter capacitieve of inductieve reactantie. De fout wordt nog beduidender bij een echte condensator of spoel. De lekweerstand of eigen weerstand maken dat er steeds met een resistief element moet rekening gehouden worden.
Ter herinnering de berekening van de reactantie:
XC = 1/ Cω
XL = L ω
waarin ω = 2 π f
Wat nu met de wet van Ohm ?
De wet van Ohm geldt in principe enkel bij gelijkstroom, maar kan aangepast aan kringen waarin de wisselstroom toegepast wordt.
Weerstand alleen volstaat niet meer als een aanduiding voor “de tegenstand” aan een wisselstroom of -spanning. Het ruimere begrip impedantie is wel correct.
We onthouden :
U = Z I
I = U / Z
Z = U / I
De waarden U en I zijn de effectieve waarden.